Project Euler

Problem 39: Integer Right Triangles

If p is the perimeter of a right angle triangle with integral length sides, {a,b,c}, there are exactly three solutions for p = 120: {20,48,52}, {24,45,51}, {30,40,50}.
For which value of p ≤ 1000, is the number of solutions maximized?

The Catch

For every value of p, how to find and check different values of the 3 sides a, b, c of a right triangle.

The Light

The 3 sides a, b, and c are related under a² + b² = c² (Pythagorean theorem) and a + b + c = p. Taking advantage of these 2 equations, we have:

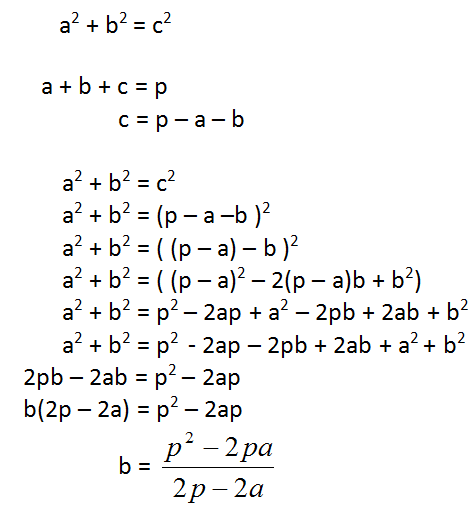
So if b is an integer, that means a, b, and c are one of p's Pythagorean triplets.

Recall:
Sum of 2 odd numbers is even.
Sum of 2 even numbers is even.
Sum of an odd and an even number is odd.
Product of 2 odd numbers is odd.
Product of 2 even numbers is even.
Product of an odd and an even number is even.

Analyzing a² + b² = c² shows that:
If a and b are both even, then c is even and p is even.
If a and b are both odd, then c is even and p is even.
If either of a or b is even and the other is odd, then c is odd and p is even.

Thus, only even values for p have Pythagorean triplets.

Since a ≤ b < c, a < p/3 because if you divide p into 3 parts, c has to always be greater than the sum of a and b.

The Code

public class Problem39
{
  public static void main(String[] args)
  {
    int max = 0;
    int maxP = 0;
    for(int p = 2; p <= 1000; p += 2)
    {
      int solution = 0;
      for(int a = 1; a < p/3; a++)       
      {
        if((p*p - 2*p*a) % (2*p - 2*a) == 0)     	  
          solution++;       
      }
      if(solution > max)
      {
        max = solution;
        maxP = p;
      }
    }
    System.out.println(maxP);
  }
}