Problem 35: Circular Primes
The number 197 is called a circular prime because all rotations of the digits: 197, 971, and 719, are themselves prime. There are thirteen such primes below 100: 2, 3, 5, 7, 11, 13, 17, 31, 37, 71, 73, 79, and 97. How many circular primes are there below one million?
The Catch
How to rotate a number.
How to speed up the execution time since the current search range is from 1 to 1,000,000. Even if only odd numbers are checked, the search range is still 500,000 iterations.
The Light
Utilizing digit-manipulating technique like in Problem 37, to rotate a number n:
- Find out how many rotation is needed. The number of rotation equals the number of digits n has. Divide (int) n by 10 to determine.
- Find a multiplier for n. The multiplier should be 10(number of digits of n).
- One of a rotated version of n = (n % 10 * multiplier) + (n/10).
- Repeat for all rotation.
For example, to rotate the number 812:
812 has 3 digits, so there must be 3 rotations (but only 2 are necessary; the number 812 itself is counted as one rotation).
Multiplier = 102 = 100
Rotate 812 = 812%10 * 100 + (int)812/10 = 200 + 81 = 281
Rotate 281 = 281%10 * 100 + (int)281/10 = 100 + 28 = 128
Rotate 128 = 812 (which is why this 3rd rotation is unnecessary).
If one digit of the number n is an even number or 5, then this number is not a prime and thus it not a circular prime.
Instead of looping through every odd, positive, natural number (which results in 500,000 iterations), loop through a list of prime numbers below an upper bound. It can be checked that this will result in only 78,498 iterations. To create this list of prime numbers, it is not efficient to loop from 2 to the upper bound and use the traditional prime check. Instead, there is a method called Sieve of Eratosthenes invented by Eratosthenes of Cyrene, a Greek mathematician.
It generates all prime numbers below 1,000,000 within 15-20 ms. The algorithm:
- Create a list of natural number from 2 to the upper bound.
- Set p = 2, the first number of the list.
- From p to the upper bound, mark p and all of its multiples.
- Set p to the next number in the list.
- Repeat step 3 and 4 until p <= sqrt(upper bound). (NOTE: some numbers will be marked several times; this is okay)
- The unmarked numbers left in the list are all prime.
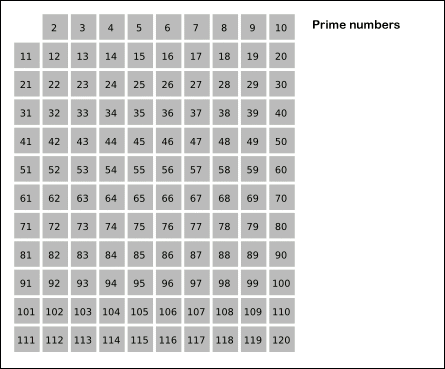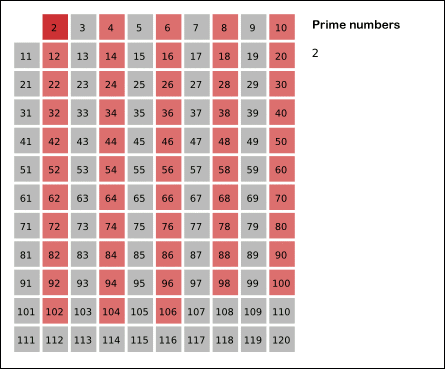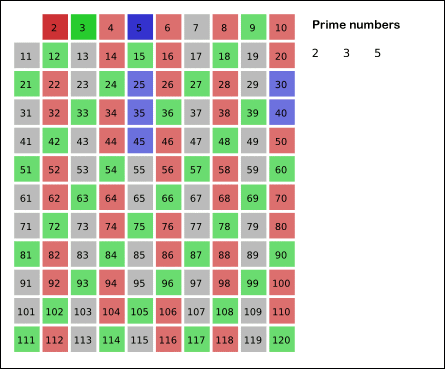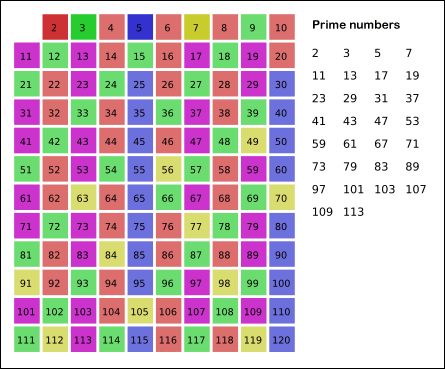
(image courtesy of Wikipedia)
When creating the Sieve of Eratosthenes, it is best to store the result in a list L. It is, however, very costly (execution-time wise) to check if a number is prime by checking if
it is in the list L. Thus, use the traditional prime check as discussed in Problem 3.
The Code
import java.util.*;
public class Problem35
{
public static void main(String[] args)
{
int count = 2; //2 and 5 will be eliminated by the last digit test. These are the only 2 exceptions.
List primeList = generatePrimes(1000000);
for(int i = 0; i < primeList.size(); i++)
{
int rotate = 0; //Number of rotations
int multiplier = 1;
int n = primeList.get(i);
boolean circularPrime = true;
boolean moveOn = false;
while(n > 0)
{
rotate++;
int lastDigit = n % 10;
n /= 10;
if(lastDigit % 2 == 0 || lastDigit == 5)
{
moveOn = true;
break;
}
multiplier *= 10;
}
if(moveOn)
continue;
multiplier /= 10;
n = primeList.get(i);
while(rotate > 0) //Last rotation is not needed
{
n = (n % 10 * multiplier) + (n/10);
rotate--;
if(!isPrime(n))
{
circularPrime = false;
break;
}
}
if(circularPrime)
count++;
}
System.out.println(count);
}
public static List generatePrimes(int max)
{
boolean[] isComposite = new boolean[max + 1];
for (int i = 2; i * i <= max; i++)
{
if (!isComposite [i])
for (int j = i; i * j <= max; j++)
{
isComposite [i*j] = true;
}
}
ArrayList list = new ArrayList();
for (int i = 2; i <= max; i++)
{
if (!isComposite [i])
list.add(new Integer(i));
}
return list;
}
public static boolean isPrime(int n)
{
if(n < 2)
return false;
if(n != 2 && n % 2 == 0)
return false;
for(int i = 3; i*i <= n; i += 2)
{
if( n % i == 0 )
return false;
}
return true;
}
}