Project Euler

Problem 18: Maximum Path Sum 1

By starting at the top of the triangle below and moving to adjacent numbers on the row below, the maximum total from top to bottom is 23.

That is, 3 + 7 + 4 + 9 = 23. Find the maximum total from top to bottom of the triangle below:

NOTE: As there are only 16384 routes, it is possible to solve this problem by trying every route. However, Problem 67, is the same challenge with a triangle containing one-hundred rows; it cannot be solved by brute force, and requires a clever method! ;o)

The Catch

If you start from the top number of the triangle like in the example provided, you end up with an incorrect answer... Why is that?
If you try every route for each level, that is 16,384 routes to check, which might take more than 1 second to execute.

The Light

The reason for your incorrect answer if you start from the top of the triangle is because of the Greedy algorithm, which is generally used to find the local extrema. For this problem, the answer should be a global extrema, or the greatest sum out of all possible routes.
For example, if the example triangle was changed to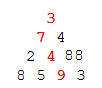then the global greatest sum is no longer 23. If you take the route 3 → 4 → 88 → 9, the correct global extrema will be 3 + 4 + 88 + 9 = 104. If you just follow the Greedy algorithm, however, you will miss better routes (just like in real life, I suppose...) To avoid the Greedy algorithm, start from the bottom of the triangle instead of from the top. We will shrink the triangle from the bottom; notice that for every 2 numbers from 2nd row downward, there is a "middle" number on the row above. For instance, 2 in 3rd row is the middle number of 8 and 5 in the 4th row and 4 from the 3rd row is the middle number of 5 and 9 from the 4th row. Starting with the most bottom row, take every 2 numbers and add each of them (separately) to their middle number. Replace their middle number with the larger sum. Repeat until the triangle is shrunk to only one number - the answer.

To demonstrate: 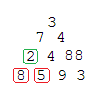8 + 2 = 10 and 5 + 2 = 7, so replace 2 with 10. Repeat for the pair 5 and 9 and 9 and 3, we have Then repeat the procedure for the 3rd row; the triangle becomes At this point, it is clear that the answer is 104, as expected.
Copy and paste the triangle to a file called "triangleInput18.txt" and use Java's Scanner class to read inputs.

The Code

import java.io.*;
import java.util.*;

public class Problem18
{
  public static void main(String[] args) throws FileNotFoundException
  {
    int row = 15;
    int rowIndex = 0;
    int[][] tri = new int[row][];

    Scanner scan = new Scanner(new File("triangleInput18.txt"));
    while(scan.hasNextLine())
    {
      String s = scan.nextLine();
      String[] input = s.split(" ");

      tri[rowIndex] = new int[input.length];
      for( int i = 0; i < input.length; i++ )       
      {
         tri[rowIndex][i] = Integer.parseInt(input[i]);
      }       
      rowIndex++;	       
    } 	     

    for(int i = row - 1; i > 0; i--)
    {
      int index = 0;
      for(int j = 0; j < tri[i].length - 1; j++, index++)       
      {
        int tmp1 = tri[i][j] + tri[i - 1][index];         
        int tmp2 = tri[i][j + 1] + tri[i - 1][index];        
        if(tmp1 > tmp2)
          tri[i - 1][index] = tmp1;
        else
          tri[i - 1][index] = tmp2;
      }  
    }
    System.out.println("Maximum total from top to bottom: " + tri[0][0]);
  }
}